Quaternions and Anim8or

A quaternion is a 4 dimensional real number. Mathematically they are an extension of the more widely used 2 dimensional complex number system. As a special case, unit quaternions, those with a magnitude of 1, are useful in representation rotations and orientations if a 3 dimensional space, allowing a simple implementation of smooth rotations along a single axis, splines, etc. Anim8or uses unit quaternions for this reason. Through this discussion the term quaternion is synonymous with unit quaternion unless otherwise indicated.

Here quaternions are shown as a 4 vector of scalar values:

Q = (x, y, z, w)

Alternate they can by represented as a 3 vector plus a scalar (a format that allows a more elegant mathematical characterization, which is not the purpose of this note):

Q = (v3, s)

I'll leave the heavy math for later.

Alternately orientations and rotations can be represents by Euler angles which are 3 vectors of real values representing the pitch (rotation about the X axis), yaw (Y axis), and roll (Z axis):

E = (p, y, r)

Here are some simple Euler rotations:

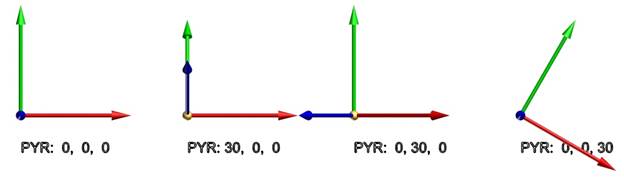
While Euler angles are easier to understand, and to relate the individual comports to our 3D world, they are difficult to interpolate smoothly and suffer from gimbal lock, a condition that prevents rotation when two axes are aligned.

Euler Rotation

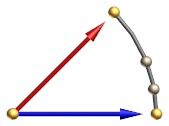
To make the discussion easier to illustrate, we'll simply the discussion to two dimensions. In a 2D Euler world an object can rotate on 2 axes. Assume that we want to smoothly rotate the sphere from its initial point indicated by the blue arrow E1 = (0, 0), to the position indicate by the red arrow E2 = (45, 0), all that's needed is to interpolate the X value from 0 to 45 (there is no rotation around the length of the arrow):

Alternately the orientation of the blue arrow could be represented by E1 = (360, 0). Then the obvious way to interpolate between would rotate in the opposite direction, making almost a full circle:

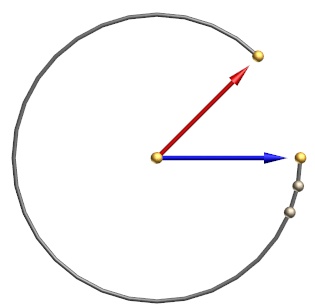
This is not what we usually want to do. However it is simple to avoid by adjusting one of the values by 360 so that |E2 - E1| < 180 before interpolating. Note that when the difference is exactly 180 there is no way to know which way the rotation should go.

As mentioned before, interpolating Euler angles in 3 dimensions is more complex, but it is not necessary to understand how to do that here.

Quaternion Rotation

Quaternion interpolation always interpolates the shortest path between values. However, it's the shortest distance in quaternion space, not necessarily the same as in 3D space. To better understand this behavior, and how to avoid undesirable rotation, we need a little more background.

Each orientation has 2 distinct quaternions. Negating all 4 scalar values does not change the orientation. That is:

Q = (x, y, z, w)   and Q' = (-x, -y, -z, -w)

are identical orientations.

Quaternions are interpolated using a function called slerp, or spherical linear interpolation

slerp(Q1, Q2, t), 0 <= t <= 1

It's not necessary at this time to understand its implementation, just to note that it smoothly rotates from one orientation to another based on the value of t.

However slerp treats Q and Q' very differently. In other words:

slerp(Q1, Q2, t)   ≠ slerp(Q1', Q2, t)

One formula rotates along the shorter path in 3D space, while the other follows the longer one. It's easier to understand how this works if you visualize an orientation as a point on the surface of a Mobius strip. As in the Euler example above, the angle around a Mobius strip represents one of the angles in an orientation. The gold and copper balls represent the same orientation but two quaternions Q1 and Q1'.

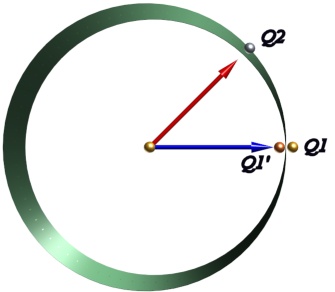
Now let's see how far, in degrees, it is from Q1to Q2. First, starting at Q1, trace a counterclockwise path around the surface. When you've traveled 45 degrees you reach Q2. Now go in the clockwise direction. When you've gone 315 degrees you reach the orientation of Q2 but you're on the opposite side of the strip. If you continue  for a total of 360 degrees until you reach the starting angle, but, again, you are on the opposite side of the strip, at Q1'. You eventually reach Q2 after traveling 675 degrees. And note that you'll need to travel 2 complete rotations, or 720 degrees, to return to the original Q1.

If you instead start at Q1' the counterclockwise direction requires 315 to reach Q2, while the clockwise direction needs 405.

How does this relate to the slerp function and Anim8or? Slerp interpolates along the shortest path between its parameters. So slerp(Q1, Q2, t) travels counterclockwise to Q2, because 45 < 315. But slerp(Q1', Q2, t) goes clockwise using a rotation of 315 degrees, since 315 < 405.

Fixing Anim8or's "Strange" Rotations

Problem:  You are creating .an8 files for an animation. You are converting Euler angles into quaternions. Occasionally between two key orientations, Qn and Qn+1, your animation unexpectedly makes an almost complete spin in the wrong direction.

What's happening: Qn+1 is incorrect. Instead you need to use Qn+1'.

How do you know when to use Q'?  Fortunately there is an easy solution. If the dot(Qn, Qn+1) < 0 then slerp(Qn, Qn+1, t) will rotate more than 180 degrees, where:

dot(Q1, Q2) = Q1.x*Q2.x + Q1.y*Q2.y + Q1.z*Q2.z + Q1wx*Q2.w

So if the dot product is negative, use Qn+1' by negating all the values in Qn+1.

--- Steve, July 18, 2015.