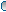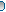I'm afraid I might not be able to finish this. I have to go to class and I might not have enough time when I return.
To at least show what I've got already, here's a wip. All that's missing are the character's really, which I've just boiled down to two.
Now that I look at it though I think it's really stretching it...
EDIT: Managed to finish it (at the expense of my painting XD)
The image needed a tad bit of photoshop color correction to fix up some lighting issue I couldn't handle within Anim8or due to using flat surfaces for leaves. You can't get a good highlight easily on the upper part of the group of leaves. (HoF contact ps.jpg)
But if photomanipulation isn't allowed on the entries then I attached an unedited one just in case. (HoF contact.jpg)
EDIT 2: Crud I rendered the wrong size. I wondered why it was so small. XD
Additional notes: Render time approx: 20 mins
This has a ton of flat surfaces for particles whatnot. I lost count how many copy pastes I did to get a clutter. And due to lack of time I couldn't fill the area with bodies. Ah well.
I found a few faults already while I stare at my screen during render. Lighting is something I should really get practicing with... well basically that here and there and I over darkened some textures for fear the characters won't stand out.
Any feedback is appreciated

Final Ver:
HoF contact ps


 Poll
Poll